Adaptive diatonic interval names/Archived version
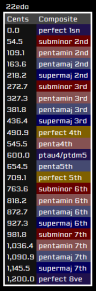
Adaptive diatonic interval names (ADIN) are Vector's attempt to characterize the labelling of certain EDOs' degrees of thirds in a manner inconsistent with conventional diatonic notation in a formal, systematic way.
Step 1: Identify central intervals
For an EDO (let's say, 58edo), identify the "central intervals" for each category. These are the diatonic neutral intervals, which may be between edosteps,
Step 2: Identify anchors
What interval qualities will label is distances from these "central intervals". For each interval degree, follow the given procedure:
- Find the smallest interval greater than or equal to 25c above the neutral interval. Take the interval BEFORE this and label it "submajor" (if its offset is still positive, otherwise, interpret it as submajor but do not actually assign it that name).
- Find a) the closest interval to 85c above the neutral interval or b) the smallest interval greater than 75c above the neutral interval, whichever is higher. Label this interval "supermajor".
- If supermajor and submajor coincide, label the interval "major" and then label the next interval up "supermajor".
- If there are no unlabelled steps between submajor and supermajor, label whichever is closer to 50c above the neutral interval "major". If this is supermajor, label the next interval up "supermajor"; if this is submajor, label the next interval down "submajor" if its offset is still positive.
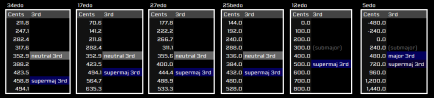
Step 3: Fill in gaps
- There should now be unlabelled steps between submajor and supermajor. These correspond to different varieties of major. Follow the table:
| Number of steps | Qualities |
|---|---|
| 1 | pentamajor |
| 2 | pentamajor, neomajor |
| 3 | pentamajor, novamajor, neomajor |
| 4 | pentamajor, novamajor, trimajor, neomajor |
| 5 | pentamajor, novamajor, trimajor, neomajor, shrubmajor |
| 6 | magimajor, pentamajor, novamajor, trimajor, neomajor, shrubmajor |
| 7 | magimajor, pentamajor, valamajor, novamajor, trimajor, neomajor, shrubmajor |
This might lead to nonsensical assignments of "pentamajor" in edos like 17 (in fact, 17 is the only edo to have this property) - but do not worry! Those will be cleaned up in later steps.
- Find the closest otherwise unlabelled interval to 103c above the neutral interval which is higher than 75c; call it "ultramajor". (Note: you may be ending up with this interval being many semitones above the neutral, that's okay because extraneous names will be clipped off once we actually apply everything to interval classes.) Label the step above ultramajor "tendo" if it is at most 1/6 of the size of the perfect fifth above neutral - otherwise, treat tendo as synonymous with the largest step that is at most 1/6 the size of the perfect fifth above neutral.
- There may now be one or more unlabelled steps between supermajor and ultramajor (ignoring tendo): this scheme currently supports one interval between these two points, which is labelled "sensamajor".
- There may also be one or more unlabelled steps below submajor. Follow the table:

Result after Step 3
| Number of steps | Qualities |
|---|---|
| 1 | tendoneutral |
| 2 | tendoneutral, supraneutral |
The neutral interval, if present in the edo, is simply called neutral.
Step 4: Repeat for minor
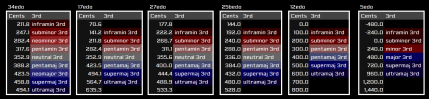
For the minor side of any interval class, swap "major" and "minor", "sub" and "super/supra" (super applies only to major and unqualified intervals, other types use supra), "ultra" and "infra", and "arto" and "tendo" (in all senses).
Step 5: Adjust fourths and fifths

The perfect fourth is, as a rule, the same degree as the diatonic minor third (whatever that happens to be) - for example, if the diatonic minor third is subminor, the perfect fourth is also interpreted as subminor, and "perfect fourth" replaces "subminor fourth". Similar logic applies for the perfect fifth and the diatonic major third.
As a result, in standard diatonic edos, "minor fourth" contracts to "fourth", and "major fifth" contracts to "fifth" For example, "subminor fourth" -> "subfourth". Instead of "minor fifth", there is "diminished fifth" (and instead of "major fourth", there is "augmented fourth").
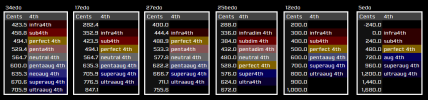
This behavior is reversed in antidiatonic edos, so that the perfect fourth is major and the perfect fifth is minor. No contraction is done in equiheptatonic edos (where the perfect fourth is neither major nor minor) or oneirotonic edos (where fifths and fourths switch places).
The semioctave may be explicitly labelled if it is present, or if two tritones are present "narrow tritone" and "wide tritone" - but these are not standard degree-based interval names.
Unisons and octaves
The unison/octave are treated as a diatonic major interval when going sharper than it, and a diatonic minor interval when going flatter than it. (Again, reversed when antidiatonic).
Composite

In order to composite our independent naming schemes for different degrees into a complete interval name list (and trim off nonsensical names near the outer edges), we'll use a system of priority. Priority starts at 0 for any neutral interval and decreases by 0.5 for every half of an edostep you travel away from the neutral (meaning that if the neutral isn't in the edo, the two closest intervals have a priority of -0.5) or more simply 1 for every edostep. The interval name with the highest priority is chosen as the canonical interval name.
If there is only one type of major or minor (not including submajor or supraminor), the qualifier on major or minor (i.e. penta- or magi-) is removed.

Functioning for various edos
| EDO | Notes |
|---|---|
| 1 | Functional: unison and octave. |
| 2 | Mostly functional: unison, octave, and tritone, which is read as a perfect fifth and perfect fourth simultaneously. |
| 3 | Oneirotonic; switches places of fifth and fourth and no perfect intervals. Neutral fifth is 400c; neutral fourth is 800c. |
| 4 | Extreme case: 300c and 900c intervals are neutral fourth and fifth respectively. Alternatively, neutral third and sixth respectively. |
| 5 | Functional as in standard notation. 4ths and fifths have exact same priority. |
| 6 | Oneirotonic; 600c interval is "supermajor" fifth. |
| 7 | Functional as in standard notation. |
| 8 | Oneirotonic; switches places of fifth and fourth and no perfect intervals. |
| 9 | Functional. Major second and minor third coincide. |
| 10 | Functional. 5edo + neutrals. |
| 11 | Functional. Most intervals are neutral. |
| 12 | Functional as in standard notation. |
| 13 | Oneirotonic; switches places of fifth and fourth and no perfect intervals. |
| 14 | Functional. 7edo + major/minor intervals which are also perfect interordinals. |
| 15 | Functional. |
| 16 | Functional. |
| 17 | Functional. Contains the nonsensical pentamajor that's resolved by the compositing process. |
| 18 | Oneirotonic; switches places of fifth and fourth and no perfect intervals. |
| 19+ | Functional. |
The first edo that the current set of names is insufficient to cover is 152edo. If an extra name is added for an interval between sensamajor and ultramajor, then the first failure is at 156, and then at 159.
Oneirotonic extension
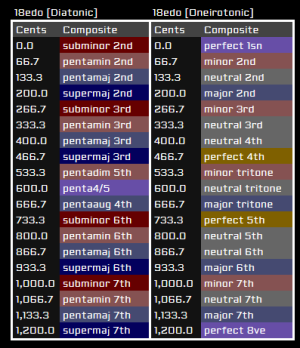
One possible extension to handle edos with an oneirotonic fifth (3, 6, 8, 13, and 18) is to use the neutralized oneirotonic scale as the basis instead of the neutralized diatonic scale. In this case, things function exactly the same as before, but based on oneirotonic instead of diatonic. The additional degree may be called a median or tritone - special tritone labels are not used as the semioctave is always the neutral tritone.
