31edo: Difference between revisions
No edit summary |
No edit summary |
||
| Line 59: | Line 59: | ||
31edo, as one of the more popular edos, has a somewhat agreed-upon notation system. This notation is simply neutral [[diatonic notation]] applied to the edo, where a half-# or half-b represents an alteration by one diesis. In this manner, all notes can be spelled in a way that does not require multiple sharps or flats. | 31edo, as one of the more popular edos, has a somewhat agreed-upon notation system. This notation is simply neutral [[diatonic notation]] applied to the edo, where a half-# or half-b represents an alteration by one diesis. In this manner, all notes can be spelled in a way that does not require multiple sharps or flats. | ||
{| class="wikitable" | |||
|+ | |||
!Step | |||
!Cents | |||
!ADIN | |||
!Neutral diatonic | |||
!Notation | |||
!Just intervals represented | |||
|- | |||
|0 | |||
|0.00 | |||
|unison | |||
|unison | |||
|A | |||
|1/1 | |||
|- | |||
|1 | |||
|38.71 | |||
|superunison | |||
|semiaugmented unison | |||
|At | |||
|49/48, 50/49, 128/125 | |||
|- | |||
|2 | |||
|77.42 | |||
|subminor second | |||
|semidiminished second | |||
|A# | |||
|25/24 | |||
|- | |||
|3 | |||
|116.13 | |||
|nearminor second | |||
|minor second | |||
|Bb | |||
|16/15 | |||
|- | |||
|4 | |||
|154.84 | |||
|neutral second | |||
|neutral second | |||
|Bd | |||
|11/10, 12/11 | |||
|- | |||
|5 | |||
|193.55 | |||
|nearmajor second | |||
|major second | |||
|B | |||
|10/9, 9/8 | |||
|- | |||
|6 | |||
|232.26 | |||
|supermajor second | |||
|semiaugmented second | |||
|Bt | |||
|8/7 | |||
|- | |||
|7 | |||
|270.97 | |||
|subminor third | |||
|semidiminished third | |||
|Cd | |||
|7/6 | |||
|- | |||
|8 | |||
|309.68 | |||
|nearminor third | |||
|minor third | |||
|C | |||
|6/5 | |||
|- | |||
|9 | |||
|348.39 | |||
|neutral third | |||
|neutral third | |||
|Ct | |||
|11/9, 16/13 | |||
|- | |||
|10 | |||
|387.10 | |||
|nearmajor third | |||
|major third | |||
|C# | |||
|5/4 | |||
|- | |||
|11 | |||
|425.81 | |||
|supermajor third | |||
|semiaugmented third | |||
|Db | |||
|9/7 | |||
|- | |||
|12 | |||
|464.52 | |||
|subfourth | |||
|semidiminished fourth | |||
|Dd | |||
|21/16, 13/10 | |||
|- | |||
|13 | |||
|503.23 | |||
|perfect fourth | |||
|perfect fourth | |||
|D | |||
|4/3 | |||
|- | |||
|14 | |||
|541.94 | |||
|neutral fourth | |||
|semiaugmented fourth | |||
|Dt | |||
|11/8, 15/11 | |||
|- | |||
|15 | |||
|580.65 | |||
|nearaugmented fourth | |||
|augmented fourth | |||
|D# | |||
|7/5 | |||
|- | |||
|16 | |||
|619.35 | |||
|neardiminished fifth | |||
|diminished fifth | |||
|Eb | |||
|10/7 | |||
|- | |||
|17 | |||
|658.06 | |||
|neutral fifth | |||
|semidiminished fifth | |||
|Ed | |||
|16/11, 22/15 | |||
|- | |||
|18 | |||
|696.77 | |||
|perfect fifth | |||
|perfect fifth | |||
|E | |||
|3/2 | |||
|- | |||
|19 | |||
|735.48 | |||
|superfifth | |||
|semiaugmented fifth | |||
|Et | |||
|32/21, 20/13 | |||
|- | |||
|20 | |||
|774.19 | |||
|subminor sixth | |||
|semidiminished sixth | |||
|Fd | |||
|14/9 | |||
|- | |||
|21 | |||
|812.90 | |||
|nearminor sixth | |||
|minor sixth | |||
|F | |||
|8/5 | |||
|- | |||
|22 | |||
|851.61 | |||
|neutral sixth | |||
|neutral sixth | |||
|Ft | |||
|13/8, 18/11 | |||
|- | |||
|23 | |||
|890.32 | |||
|nearmajor sixth | |||
|major sixth | |||
|F# | |||
|5/3 | |||
|- | |||
|24 | |||
|929.03 | |||
|supermajor sixth | |||
|semiaugmented sixth | |||
|Gb | |||
|12/7 | |||
|- | |||
|25 | |||
|967.74 | |||
|subminor seventh | |||
|semidiminished seventh | |||
|Gd | |||
|7/4 | |||
|- | |||
|26 | |||
|1,006.45 | |||
|nearminor seventh | |||
|minor seventh | |||
|G | |||
|9/5, 16/9 | |||
|- | |||
|27 | |||
|1,045.16 | |||
|neutral seventh | |||
|neutral seventh | |||
|Gt | |||
|11/6, 20/11 | |||
|- | |||
|28 | |||
|1,083.87 | |||
|nearmajor seventh | |||
|major seventh | |||
|G# | |||
|15/8 | |||
|- | |||
|29 | |||
|1,122.58 | |||
|supermajor seventh | |||
|semiaugmented seventh | |||
|Ab | |||
|48/25 | |||
|- | |||
|30 | |||
|1,161.29 | |||
|suboctave | |||
|semidiminished octave | |||
|Ad | |||
|49/25, 125/64, 96/49 | |||
|- | |||
|31 | |||
|1,200.00 | |||
|octave | |||
|octave | |||
|A | |||
|2/1 | |||
|} | |||
{{Cat|Edos}} | {{Cat|Edos}} | ||
Revision as of 02:21, 14 February 2026
31edo, or 31 equal divisions of the octave, is an equal tuning with a step size of approximately 39 cents. Aside from 12edo, it is a popular tuning of Meantone and has accurate approximations of harmonics 5 and 7.
Theory
Edostep interpretations
31edo's edostep has the following interpretations in the 2...13 subgroup:
- 49/48 (the difference between 7/6 and 8/7)
- 50/49 (the difference between 7/5 and 10/7)
- 64/63 (the difference between 8/7 and 9/8)
- 36/35 (the difference between 7/6 and 6/5)
- 54/55 (the difference between 6/5 and 11/9)
- 45/44 (the difference between 5/4 and 11/9)
- 128/125 (the difference between 5/4 and 32/25)
- 65/64 (the difference between 16/13 and 5/4)
JI approximation
31edo is best understood as a 2.3.5.7.11.23 system, although it has a sharp but functional prime 13. The flatness of harmonics 9 and 11 mostly cancel out, producing a close-to-pure ~11/9 neutral interval. It has a rather functional diatonic scale, with the whole tone split into 2 and 3, with 2 steps making a chromatic semitone (or "chromatone") and 3 steps making a diatonic semitone (or "diatone").
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | 0.0 | -5.2 | +0.8 | -1.1 | -9.4 | +11.1 | +11.2 | +12.2 | -8.9 | +15.6 | +16.3 |
| Relative (%) | 0.0 | -13.4 | +2.0 | -2.8 | -24.2 | +28.6 | +28.9 | +31.4 | -23.0 | +40.3 | +42.0 | |
| Steps
(reduced) |
31
(0) |
49
(18) |
72
(10) |
87
(25) |
107
(14) |
115
(22) |
127
(3) |
132
(8) |
140
(16) |
151
(27) |
154
(30) | |
| Quality | Subminor | Pentaminor | Neutral | Pentamajor | Supermajor |
|---|---|---|---|---|---|
| Cents | 271 | 310 | 348 | 387 | 426 |
| Just interpretation | 7/6 | 6/5 | 11/9 | 5/4 | 9/7 |
Diatonic thirds are bolded.
Chords
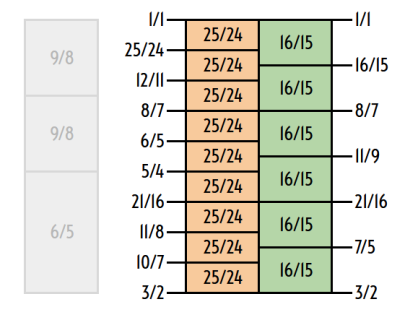
Along with its diatonic major and minor chords which approximate 5-limit harmony, 31edo also has a narrow but functional supermajor triad, and a well-tuned subminor triad. It also supports arto and tendo chords, with its slendric chords of [0 6 18] and [0 12 18], and has a neutral triad [0 9 18] which represents both artoneutral and tendoneutral triads in the 11- and 13-limit.
Scales
31edo does not temper out 64/63, meaning that it can be used to tune Diasem while representing some simpler 5-limit intervals. 31edo's step is called a diesis, and can function as an aberrisma. Due to being a prime number, 31edo has a large number of full-period MOS scales that exist in the edo. Orwell[9] (gramitonic) is one example, so is Mohajira[7] (mosh).
31edo also has a usable 12-note chromatic scale, approximating golden Meantone/monocot.
Regular temperaments
Besides Meantone (for which it provides an excellent tuning and which is shared with 19edo), 31edo also supports variations of Rastmic temperament (like 24edo), Slendric (like 36edo), Miracle (like 41edo), and Orwell (like 22edo).
Notation
31edo, as one of the more popular edos, has a somewhat agreed-upon notation system. This notation is simply neutral diatonic notation applied to the edo, where a half-# or half-b represents an alteration by one diesis. In this manner, all notes can be spelled in a way that does not require multiple sharps or flats.
| Step | Cents | ADIN | Neutral diatonic | Notation | Just intervals represented |
|---|---|---|---|---|---|
| 0 | 0.00 | unison | unison | A | 1/1 |
| 1 | 38.71 | superunison | semiaugmented unison | At | 49/48, 50/49, 128/125 |
| 2 | 77.42 | subminor second | semidiminished second | A# | 25/24 |
| 3 | 116.13 | nearminor second | minor second | Bb | 16/15 |
| 4 | 154.84 | neutral second | neutral second | Bd | 11/10, 12/11 |
| 5 | 193.55 | nearmajor second | major second | B | 10/9, 9/8 |
| 6 | 232.26 | supermajor second | semiaugmented second | Bt | 8/7 |
| 7 | 270.97 | subminor third | semidiminished third | Cd | 7/6 |
| 8 | 309.68 | nearminor third | minor third | C | 6/5 |
| 9 | 348.39 | neutral third | neutral third | Ct | 11/9, 16/13 |
| 10 | 387.10 | nearmajor third | major third | C# | 5/4 |
| 11 | 425.81 | supermajor third | semiaugmented third | Db | 9/7 |
| 12 | 464.52 | subfourth | semidiminished fourth | Dd | 21/16, 13/10 |
| 13 | 503.23 | perfect fourth | perfect fourth | D | 4/3 |
| 14 | 541.94 | neutral fourth | semiaugmented fourth | Dt | 11/8, 15/11 |
| 15 | 580.65 | nearaugmented fourth | augmented fourth | D# | 7/5 |
| 16 | 619.35 | neardiminished fifth | diminished fifth | Eb | 10/7 |
| 17 | 658.06 | neutral fifth | semidiminished fifth | Ed | 16/11, 22/15 |
| 18 | 696.77 | perfect fifth | perfect fifth | E | 3/2 |
| 19 | 735.48 | superfifth | semiaugmented fifth | Et | 32/21, 20/13 |
| 20 | 774.19 | subminor sixth | semidiminished sixth | Fd | 14/9 |
| 21 | 812.90 | nearminor sixth | minor sixth | F | 8/5 |
| 22 | 851.61 | neutral sixth | neutral sixth | Ft | 13/8, 18/11 |
| 23 | 890.32 | nearmajor sixth | major sixth | F# | 5/3 |
| 24 | 929.03 | supermajor sixth | semiaugmented sixth | Gb | 12/7 |
| 25 | 967.74 | subminor seventh | semidiminished seventh | Gd | 7/4 |
| 26 | 1,006.45 | nearminor seventh | minor seventh | G | 9/5, 16/9 |
| 27 | 1,045.16 | neutral seventh | neutral seventh | Gt | 11/6, 20/11 |
| 28 | 1,083.87 | nearmajor seventh | major seventh | G# | 15/8 |
| 29 | 1,122.58 | supermajor seventh | semiaugmented seventh | Ab | 48/25 |
| 30 | 1,161.29 | suboctave | semidiminished octave | Ad | 49/25, 125/64, 96/49 |
| 31 | 1,200.00 | octave | octave | A | 2/1 |
