15edo: Difference between revisions
Tristanbay (talk | contribs) →JI approximation: fixed table header |
fixed the "15" bug hopefully |
||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:HarmonicTable15.png|thumb|478x478px|The 2-dimensional harmonic table that serves as 15edo's defining feature.]] | |||
'''15edo''', or 15 equal divisions of the octave, is the equal tuning featuring steps of (1200/15) = 80 cents, 15 of which stack to the perfect octave [[2/1]]. It is notable for its acceptable but rather distant approximation of the 11-limit featuring a near-isoharmonic 4:5:6, and for its contorted mappings. | '''15edo''', or 15 equal divisions of the octave, is the equal tuning featuring steps of (1200/15) = 80 cents, 15 of which stack to the perfect octave [[2/1]]. It is notable for its acceptable but rather distant approximation of the 11-limit featuring a near-isoharmonic 4:5:6, and for its contorted mappings. | ||
== Theory == | == Theory == | ||
==== Edostep interpretations ==== | |||
15edo's edostep has the following interpretations in the 2...11 subgroup: | |||
* 16/15 (the difference between 5/4 and 4/3) | |||
* 25/24 (the difference between 5/4 and 6/5) | |||
* 81/80 (the difference between 9/8 and 10/9) | |||
* 36/35 (the difference between 5/4 and 9/7) | |||
* 22/21 (the difference between 7/6 and 11/9) | |||
==== JI approximation ==== | ==== JI approximation ==== | ||
15edo has roughly 10-20% error on prime harmonics 3 through 11, which is a deviation from just intonation significant enough to severely affect its structure, without fully compromising the function of the prime harmonics. It is best seen as a crude approximation of the 11-limit. Because it is not a meantone system, the best diatonic to use for 5-limit harmony is the Zarlino diatonic scale (LMsLMLs), tuned in 15edo as 3-2-1-3-2-3-1. Note that 15edo lacks a standard MOS diatonic scale due to its [[Perfect fifth|fifth]] being 720 cents. | 15edo has roughly 10-20% error on prime harmonics 3 through 11, which is a deviation from just intonation significant enough to severely affect its structure, without fully compromising the function of the prime harmonics. It is best seen as a crude approximation of the 11-limit. Because it is not a meantone system, the best diatonic to use for 5-limit harmony is the Zarlino diatonic scale (LMsLMLs), tuned in 15edo as 3-2-1-3-2-3-1. Note that 15edo lacks a standard MOS diatonic scale due to its [[Perfect fifth|fifth]] being 720 cents. | ||
Significantly, 15edo is 5 x 3, and inherits its tunings of 3 and 7 from 5edo, and 5 from 3edo. This requires either a chain of 11/8s or 23/16 or a 2-dimensional lattice be used to visualize 15edo's structure in a similar manner to the circle of fifths in 12edo. | Significantly, 15edo is 5 x 3, and inherits its tunings of 3 and 7 from 5edo, and 5 from 3edo. This requires either a chain of 11/8s or 23/16 or a 2-dimensional lattice be used to visualize 15edo's structure in a similar manner to the circle of fifths in 12edo. | ||
{{Harmonics in ED|15|31|0}} | |||
{| class="wikitable" | |||
|+Thirds in 15edo | |||
!Quality | |||
|Minor | |||
|Major | |||
|- | |||
!Cents | |||
|320 | |||
|400 | |||
|- | |||
!Just interpretation | |||
|6/5 | |||
|5/4 | |||
|} | |||
==== Chords ==== | |||
15edo contains 5edo's suspended triads, now functioning as a kind of "tendo and arto" triads. However, it adds to 5edo standard major and minor triads. Its major triad is especially notable for being close to an isoharmonic 50:63:76 triad, a property not shared by either other 5n-edos like 25 or 12edo. Additionally, the wolf chords coming with the Zarlino diatonic have a wolf fifth of 640 cents, which is also the tuning for 16/11 and thus significantly more functional than the wolf fifth in diatonic is in general. Additionally, 15edo approximates the harmonic tetrad 4:5:6:7 as [0 5 9 12]. 9:10:11:12 is equidistant (spanning a perfect fourth), and so is 6:7:8:9 (spanning a perfect fifth). | |||
== Intervals == | |||
=== Interval categories === | |||
Here is a table of 15edo's intervals: | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
! | !Name | ||
!Degree | |||
!Cents | |||
!Approximate Ratios | |||
|- | |||
|Unison | |||
|0 | |||
|0 | |||
|1/1 | |||
|- | |||
|Minor second | |||
|1 | |||
|80 | |||
|'''25/24,''' 16/15 | |||
|- | |||
|Small major second | |||
|2 | |||
|160 | |||
|'''10/9''' | |||
|- | |||
|Large major second | |||
|3 | |||
|240 | |||
|'''8/7''', 9/8 | |||
|- | |||
|Minor third | |||
|4 | |||
|320 | |||
|'''6/5''' | |||
|- | |||
|Major third | |||
|5 | |||
|400 | |||
|'''5/4''' | |||
|- | |||
|Perfect fourth | |||
|6 | |||
|480 | |||
|'''4/3''', 21/16 | |||
|- | |||
|Small tritone (acute fourth) | |||
|7 | |||
|560 | |||
|'''11/8''', 7/5 | |||
|- | |||
|Large tritone (grave fifth) | |||
|8 | |||
|640 | |||
|'''16/11''', 10/7 | |||
|- | |||
|Perfect fifth | |||
|9 | |||
|720 | |||
|'''3/2''', 32/21 | |||
|- | |||
|Minor sixth | |||
|10 | |||
|800 | |||
|'''8/5''' | |||
|- | |||
|Major sixth | |||
|11 | |||
|880 | |||
|'''5/3''' | |||
|- | |||
|Narrow minor seventh | |||
|12 | |||
|960 | |||
|'''7/4''', 16/9 | |||
|- | |- | ||
|Wide minor seventh | |||
|13 | |||
|1040 | |||
| | |'''9/5''' | ||
| | |||
| | |||
|- | |- | ||
|Major seventh | |||
| | |14 | ||
| | |1120 | ||
|'''48/25,''' 15/8 | |||
| | |||
| | |||
|- | |- | ||
|Octave | |||
|15 | |15 | ||
|1200 | |||
|2/1 | |||
| | |||
| | |||
|} | |} | ||
=== The harmonic table === | |||
In 12edo, we often arrange intervals on a "circle of fifths", which outlines a lot of the harmonic structure we use in that tuning. In 15edo, a circle of fifths doesn't end up covering all the intervals (as it repeats after 5 steps), so we might think to use a circle of major thirds, the next simplest interval in terms of JI, but as it turns out, that ALSO doesn't cover all the intervals, repeating after only 3 steps. And with harmonic sevenths, we're back to looping after 5 again. As such, 15edo can be described as "contorted" in 2.3.7 and 2.5. So, the only solution (other than stacking the harmonic 11) is to use a two-dimensional "circle", which forms a '''torus'''-shaped "harmonic table": | |||
{| class="wikitable" | |||
|+ | |||
|'''0c''' | |||
|400c | |||
|800c | |||
|'''0c''' | |||
|400c | |||
|800c | |||
|'''0c''' | |||
|- | |||
|480c | |||
|880c | |||
|80c | |||
|480c | |||
|880c | |||
|80c | |||
|480c | |||
|- | |||
|960c | |||
|160c | |||
|560c | |||
|960c | |||
|160c | |||
|560c | |||
|960c | |||
|- | |||
|240c | |||
|640c | |||
|1040c | |||
|240c | |||
|640c | |||
|1040c | |||
|240c | |||
|- | |||
|720c | |||
|1120c | |||
|320c | |||
|720c | |||
|1120c | |||
|320c | |||
|720c | |||
|- | |||
|'''0c''' | |||
|400c | |||
|800c | |||
|'''0c''' | |||
|400c | |||
|800c | |||
|'''0c''' | |||
|- | |||
|480c | |||
|880c | |||
|80c | |||
|480c | |||
|880c | |||
|80c | |||
|480c | |||
|- | |||
|960c | |||
|160c | |||
|560c | |||
|960c | |||
|160c | |||
|560c | |||
|960c | |||
|- | |||
|240c | |||
|640c | |||
|1040c | |||
|240c | |||
|640c | |||
|1040c | |||
|240c | |||
|- | |||
|720c | |||
|1120c | |||
|320c | |||
|720c | |||
|1120c | |||
|320c | |||
|720c | |||
|- | |||
|'''0c''' | |||
|400c | |||
|800c | |||
|'''0c''' | |||
|400c | |||
|800c | |||
|'''0c''' | |||
|} | |||
We call this a torus because it wraps around from one side to the other, like if you were to print this on the surface of a donut. | |||
Here, | |||
* fifths are found by stepping 1 step up the Y-axis. | |||
* harmonic sevenths are found by stepping 2 steps down the Y-axis. | |||
* major thirds are found by stepping 1 step right along the X-axis. | |||
==== | Instead of two types of semitones, 15edo has four: | ||
* the limma, found by stepping down and to the left by 1 on the table. This separates intervals belonging to different classes. | |||
* the classical chroma, found by stepping down 1 and right 2 on the table. This separates intervals with the same class, but different qualities. | |||
* the syntonic comma, found by stepping up 4 and left 1 on the table. This separates standard intervals from "wolf" intervals. | |||
* the diaschisma, found by stepping up 4 and right 2 on the table. This separates fifth-generated "diatonic" intervals and their augmented or diminished zarlino counterparts. Note that this semitone is actually the ''complement'' of the just diaschisma, since the diaschisma proper is a negative interval in 15edo. | |||
== Scales == | |||
The Zarlino diatonic scale LmsLmLs or LsmLmLs is a way to preserve the classic major and minor dichotomies from 12edo. In the fourteen modes of these two scales, all thirds (i. e. intervals formable by ascending two scale-steps) are either major or minor, all fourths are either perfect fourths or large tritones, all fifths are perfect fifths or small tritones, and all sixths are either major or minor, with the following exceptions: | |||
* in two of the fourteen modes, the fifth (i. e. interval formable by ascending four scale-steps) above the tonic is the 640c interval | |||
* in two of the fourteen modes, the fourth is the 560c interval | |||
* in two of the fourteen modes, the sixth is the 960c interval | |||
* in two of the fourteen modes, the third is the 240c interval. | |||
All of these exceptions involve intervals that can be better interpreted using intervals containing prime factors 7 and 11; thus, the Zarlino diatonic scale can bridge the classical 5-limit JI intervals with more complex intervals. | |||
There is no MOS diatonic scale in 15edo, because a MOS diatonic scale is generated by stacking the fifth six times to get seven pitch classes, but in 15edo the process of stacking the fifth can only generate five pitch classes. | |||
=== Non-diatonic scales === | |||
The scales generated by stacking the small major second, which are denoted "porcupine scales" due to their connection with the rank-2 [[regular temperament]] "porcupine", are onyx ({{Interval ruler|15|0, 160, 320, 480, 720, 880, 1040, 1200}}) and pine ({{Interval ruler|15|0, 160, 320, 480, 640, 720, 880, 1040, 1200}}). The steps of the porcupine scales are minor tones. In onyx, four notes have perfect fifths above them, and four notes have perfect fourths, overlapping at one note which has both. Onyx has a special relationship to the diatonic scale, however, and this can be found by sharping the third and seventh degrees of onyx to produce the zarlino diatonic scale. The pine scale is simply the onyx scale with an extra note, which could function similarly to a "blue note" in blues. | |||
The scales generated by stacking the 320-cent minor third are called smitonic ({{Interval ruler|15|0, 80, 320, 400, 640, 720, 960, 1200}}) and 4L 7s ({{Interval ruler|15|0, 80, 160, 320, 400, 480, 640, 720, 800, 960, 1040, 1200}}), with the latter sort of functioning as a chromatic scale of the former. Smitonic contains a singular perfect fifth, where a 320-cent minor third and 400-cent major third span the same number of scale steps; in general, smitonic contains many intervals close to JI ratios in the 5-limit and 7-limit. | |||
The scales generated by stacking either tritone are called pentic ({{Interval ruler|15|0, 80, 560, 640, 720, 1200}}), antidiatonic ({{Interval ruler|15|0, 80, 160, 560, 640, 720, 800, 1200}}), balzano ({{Interval ruler|15|0, 80, 160, 240, 560, 640, 720, 800, 880, 1200}}), and 2L 9s ({{Interval ruler|15|0, 80, 160, 240, 320, 560, 640, 720, 800, 880, 960, 1200}}). | |||
After this, we have two special families of scales: augmented and blackwood. We will start off with blackwood. | |||
==== Blackwood ==== | |||
Blackwood is based on our "fifth-generated diatonic" {{Interval ruler|15|0, 240, 480, 720, 960, 1200}}. If we split each step of this scale into a larger and smaller portion, we get the blackwood scale proper: {{Interval ruler|15|0, 160, 240, 400, 480, 640, 720, 880, 960, 1120, 1200}}. This scale has only two modes: major and minor, but it is extremely significant if you're used to diatonic harmony, since it has the unique property of always having either a major triad or a minor triad on any given note. In fact, by adding "missing" notes to zarlino to ensure that (which happen to themselves be in the shape of a major chord), we get blackwood. Thus, the blackwood scale can serve as an extremely powerful alternative to the absent MOS diatonic of this edo - it is, in a sense, a "purer" version of said system. (In other edos, this scale's relation to zarlino generalizes to that of [[blackdye]], which loses some of its structural elegance in favor of a more direct diatonic connection and more in-tune intervals.) | |||
==== Augmented ==== | |||
Augmented is, conversely, based on major thirds. The basic augmented scale is {{{Interval ruler|15|0, 400, 800, 1200}}}, which is equivalent to 12edo's augmented triad. We can follow the same formula as blackwood and split this scale into large and small steps to get the following possible combinations: | |||
- {{Interval ruler|15|0, 320, 400, 720, 800, 1120, 1200}} - the augmented scale proper, which contains fifths on exactly three of the six notes. 12edo contains a tuning of this scale, but we usually don't talk about it in 12edo. | |||
- {{Interval ruler|15|0, 240, 400, 640, 800, 1040, 1200}} - the wholetone scale, which alternates the two sizes of wholetones and which contains many 7-limit intervals, but no fifths. This is similar to 12edo's wholetone scale, but since there are two different kinds of wholetones in 15edo, it uses both. | |||
- {{Interval ruler|15|0, 160, 320, 400, 560, 720, 800, 960, 1120, 1200}} - the hyrulic scale, which is a way of combining the two prior scales to form a 9-note scale. This can be thought of as having perfect thirds, and major and minor fifths. | |||
- {{Interval ruler|15|0, 240, 320, 400, 640, 720, 800, 1040, 1120, 1200}} - the tcherepnin scale, which is another combination of hard and soft triwood. This can also be thought of as having similar harmony to hyrulic, but with the minor fifth one step flatter. | |||
=== MODMOS structures === | |||
Let's take the minor scale: | |||
{{Interval ruler|15|0, 240, 320, 480, 720, 800, 1040, 1200}} - minor | |||
A common way to alter the minor scale is to sharpen the sixth and/or seventh degrees, resulting in the harmonic and melodic minor and variations of Dorian: | |||
{{Interval ruler|15|0, 240, 320, 480, 720, 800, 1120, 1200}} - harmonic minor | |||
{{Interval ruler|15|0, 240, 320, 480, 720, 880, 1120, 1200}} - dark melodic minor | |||
{{Interval ruler|15|0, 240, 320, 480, 720, 960, 1120, 1200}} - bright melodic minor | |||
{{Interval ruler|15|0, 240, 320, 480, 720, 880, 1040, 1200}}- "diatonyx" dorian | |||
{{Interval ruler|15|0, 240, 320, 480, 720, 960, 1040, 1200}} - didymian dorian | |||
A scale with a single generator (octave-equivalent, of course) is called a "MOS", and all these scales, including normal zarlino, are "MODMOSes" of '''onyx''', formed by sharping or flatting a few notes of it respectively. While technically, because this is an equal tuning, any 7-note scale can be a MODMOS of onyx, I try to reserve it for scales that have harmonic commonalities with diatonic or with onyx. | |||
=== Constructing chords and splitting steps === | |||
A more interesting way to construct scales is to stack chords rather than single intervals. For example, if we stack 3 major chords, we get: | |||
{{Interval ruler|15|0, 400, 720, 1200}} (major chord on root) | |||
+ {{Interval ruler|15|240, 720, 1120}} (major chord on fifth) | |||
+ {{Interval ruler|15|0, 480, 880, 1200}} (major chord descending from root) | |||
= {{Interval ruler|15|0, 240, 400, 480, 720, 880, 1120, 1200}} - major | |||
Surprise! Here's the zarlino scale again. | |||
Let's try minor chords. This corresponds to flatting the seventh, third, and sixth degrees by one step. | |||
{{Interval ruler|15|0, 240, 320, 480, 720, 800, 1040, 1200}}- minor | |||
In fact, this is actually how the normal major and minor scales are constructed in diatonic, so it's neat to see that it checks out here. | |||
So instead, let's try a different chord (let's say, for some reason, you cared a lot about wolf chords). | |||
{{Interval ruler|15|0, 400, 640, 1200}} (wolf major chord on root) | |||
+ {{Interval ruler|15|80, 640, 1040}} (wolf major chord on wolf fifth) | |||
+ {{Interval ruler|15|0, 560, 960, 1200}} (wolf major chord descending from root) | |||
= {{Interval ruler|15|0, 80, 400, 560, 640, 960, 1040, 1200}} - wolf major | |||
You can call this the "wolf major scale" because of how it's constructed. | |||
Let's try a kind of diminished chord, called a wolf diminished chord, made of two different sizes of minor third. Since the chord is a lot narrower, we'll need 4 chords instead of 3 to build a reasonable scale. | |||
{{Interval ruler|15|0, 240, 560, 1200}} (wolf diminished chord on root) | |||
+ {{Interval ruler|15|560, 800, 1120}} (wolf diminished chord on dim fifth) | |||
+ {{Interval ruler|15|0, 640, 880, 1200}} (wolf diminished chord descending from root) | |||
+ {{Interval ruler|15|80, 320, 640}} (wolf diminished chord descending from aug fourth) | |||
= {{Interval ruler|15|0, 80, 240, 320, 560, 640, 800, 880, 1120, 1200}}- diminished | |||
This scale also contains a "major wolf diminished" chord, which corresponds to the harmonic series sequence 5:6:7, much like a normal major chord corresponds to 4:5:6. | |||
As can be seen, there's a lot of possibilities here. | |||
Another way to build scales is by choosing a few key intervals, and splitting the jumps between them into steps. For example, we might decide that our key notes are {{{Interval ruler|15|0, 400, 480, 720, 1200}}}. | |||
Here, we have two large jumps that can be split into steps, and there's a couple ways to do this, including ones that just result in zarlino and ones that result in scales we haven't seen before. | |||
{{Interval ruler|15|0, 240, 400, 480, 720, 960, 1200}}- zaretan | |||
{{Interval ruler|15|0, 160, 400, 480, 720, 960, 1200}} - legatus | |||
{{Interval ruler|15|0, 240, 400, 480, 720, 960, 1040, 1200}}- decurion | |||
{{Interval ruler|15|0, 160, 400, 480, 720, 960, 1040, 1200}} - kaiser | |||
If we choose a different set of key intervals, we get a different set of possible scales: | |||
{{Interval ruler|15|0, 240, 400, 960, 1200}} = | |||
{{Interval ruler|15|0, 240, 400, 800, 640, 960, 1200}} - anhedonia | |||
{{Interval ruler|15|0, 240, 400, 880, 720, 540, 960, 1200}} - mok | |||
{{Interval ruler|15|0, 560, 400, 960, 1200}} = | |||
{{Interval ruler|15|0, 240, 560, 400, 720, 960, 1200}}- amsel | |||
{{Interval ruler|15|0, 320, 560, 400, 1120, 880, 960, 1200}} - drossel | |||
=== Periodicity blocks === | |||
In 15edo, there are four primary ways of reaching the semitone on the harmonic table, corresponding to different copies of the semitone repeating periodically near the unison. It can be found as the difference between a stack of two fifths and a minor tone (the syntonic comma), the difference between a major third and a perfect fourth (the limma), the difference between the two tritones (the diaschisma), and the difference between a major and minor third (the classical chroma). | |||
The standard zarlino scale can be defined by having the classical chroma and syntonic comma as its "chromas": if we create a tile that repeats at each multiple of these two chromas, the intervals within that tile are precisely those in the zarlino scale. | |||
However, we can choose a different pair of semitones as our chromas, and get a different scale. Here's the classical chroma x diaschisma scale. | |||
{{Interval ruler|15|0, 240, 320, 400, 560, 640, 800, 960, 1040, 1120, 1200}} - elena | |||
{{Interval ruler|15|0, 240, 320, 400, 560, 720, 800, 960, 1040, 1120, 1200}} - kee'ra* | |||
''*Note: in just intonation, the [[Collection of scales|kee'ra]] scale is a 7-limit "chair" scale, not a 5-limit periodicity block.'' | |||
There are two variants as, since the diaschisma can be created by stacking two augmented fourths, the augmented fourth and diminished fifth fall precisely on the edge. | |||
[[File:Valentine.png|thumb|A comparison of 15edo and 16edo, showing their similarities (see [[Carlos Alpha]]) and 15edo's "Onyx" scale.]] | |||
And the classical chroma x limma scale: | |||
{{Interval ruler|15|0, 320, 560, 800, 1040, 1200}}- myn | |||
=== Regular temperaments === | === Regular temperaments === | ||
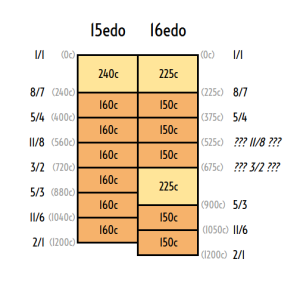
15edo shares Porcupine with 22edo, Augmented with 12edo, Semaphore with | 15edo shares Porcupine with 22edo, Augmented with 12edo, Semaphore with 19edo, and Blackwood with 10edo. It is also a tuning of [[Carlos Alpha]], like [[16edo]]. | ||
== Notation == | == Notation == | ||
Due to MOS-diatonic-based notations being nonfunctional with edos that have multiple chains of fifths (except for [[Diatonic notation#Ups and downs notation|ups and downs notation]], and even that requires E and F be treated as enharmonic), they are somewhat inconvenient for working with 15edo. Notation is often [[Notation#KISS notation|KISS notation]] based on onyx or pentawood, or notation based on the Zarlino diatonic scale. | Due to MOS-diatonic-based notations being nonfunctional with edos that have multiple chains of fifths (except for [[Diatonic notation#Ups and downs notation|ups and downs notation]], and even that requires E and F be treated as enharmonic), they are somewhat inconvenient for working with 15edo. Notation is often [[Notation#KISS notation|KISS notation]] based on onyx or pentawood, or notation based on the Zarlino diatonic scale. | ||
{{Cat|Edos}} | |||
Latest revision as of 21:13, 8 February 2026

15edo, or 15 equal divisions of the octave, is the equal tuning featuring steps of (1200/15) = 80 cents, 15 of which stack to the perfect octave 2/1. It is notable for its acceptable but rather distant approximation of the 11-limit featuring a near-isoharmonic 4:5:6, and for its contorted mappings.
Theory
Edostep interpretations
15edo's edostep has the following interpretations in the 2...11 subgroup:
- 16/15 (the difference between 5/4 and 4/3)
- 25/24 (the difference between 5/4 and 6/5)
- 81/80 (the difference between 9/8 and 10/9)
- 36/35 (the difference between 5/4 and 9/7)
- 22/21 (the difference between 7/6 and 11/9)
JI approximation
15edo has roughly 10-20% error on prime harmonics 3 through 11, which is a deviation from just intonation significant enough to severely affect its structure, without fully compromising the function of the prime harmonics. It is best seen as a crude approximation of the 11-limit. Because it is not a meantone system, the best diatonic to use for 5-limit harmony is the Zarlino diatonic scale (LMsLMLs), tuned in 15edo as 3-2-1-3-2-3-1. Note that 15edo lacks a standard MOS diatonic scale due to its fifth being 720 cents. Significantly, 15edo is 5 x 3, and inherits its tunings of 3 and 7 from 5edo, and 5 from 3edo. This requires either a chain of 11/8s or 23/16 or a 2-dimensional lattice be used to visualize 15edo's structure in a similar manner to the circle of fifths in 12edo.
| Harmonic | 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Absolute (¢) | 0.0 | +18.0 | +13.7 | -8.8 | +8.7 | +39.5 | -25.0 | +22.5 | +11.7 | +10.4 | -25.0 |
| Relative (%) | 0.0 | +22.6 | +17.1 | -11.0 | +10.9 | +49.3 | -31.2 | +28.1 | +14.7 | +13.0 | -31.3 | |
| Steps
(reduced) |
15
(0) |
24
(9) |
35
(5) |
42
(12) |
52
(7) |
56
(11) |
61
(1) |
64
(4) |
68
(8) |
73
(13) |
74
(14) | |
| Quality | Minor | Major |
|---|---|---|
| Cents | 320 | 400 |
| Just interpretation | 6/5 | 5/4 |
Chords
15edo contains 5edo's suspended triads, now functioning as a kind of "tendo and arto" triads. However, it adds to 5edo standard major and minor triads. Its major triad is especially notable for being close to an isoharmonic 50:63:76 triad, a property not shared by either other 5n-edos like 25 or 12edo. Additionally, the wolf chords coming with the Zarlino diatonic have a wolf fifth of 640 cents, which is also the tuning for 16/11 and thus significantly more functional than the wolf fifth in diatonic is in general. Additionally, 15edo approximates the harmonic tetrad 4:5:6:7 as [0 5 9 12]. 9:10:11:12 is equidistant (spanning a perfect fourth), and so is 6:7:8:9 (spanning a perfect fifth).
Intervals
Interval categories
Here is a table of 15edo's intervals:
| Name | Degree | Cents | Approximate Ratios |
|---|---|---|---|
| Unison | 0 | 0 | 1/1 |
| Minor second | 1 | 80 | 25/24, 16/15 |
| Small major second | 2 | 160 | 10/9 |
| Large major second | 3 | 240 | 8/7, 9/8 |
| Minor third | 4 | 320 | 6/5 |
| Major third | 5 | 400 | 5/4 |
| Perfect fourth | 6 | 480 | 4/3, 21/16 |
| Small tritone (acute fourth) | 7 | 560 | 11/8, 7/5 |
| Large tritone (grave fifth) | 8 | 640 | 16/11, 10/7 |
| Perfect fifth | 9 | 720 | 3/2, 32/21 |
| Minor sixth | 10 | 800 | 8/5 |
| Major sixth | 11 | 880 | 5/3 |
| Narrow minor seventh | 12 | 960 | 7/4, 16/9 |
| Wide minor seventh | 13 | 1040 | 9/5 |
| Major seventh | 14 | 1120 | 48/25, 15/8 |
| Octave | 15 | 1200 | 2/1 |
The harmonic table
In 12edo, we often arrange intervals on a "circle of fifths", which outlines a lot of the harmonic structure we use in that tuning. In 15edo, a circle of fifths doesn't end up covering all the intervals (as it repeats after 5 steps), so we might think to use a circle of major thirds, the next simplest interval in terms of JI, but as it turns out, that ALSO doesn't cover all the intervals, repeating after only 3 steps. And with harmonic sevenths, we're back to looping after 5 again. As such, 15edo can be described as "contorted" in 2.3.7 and 2.5. So, the only solution (other than stacking the harmonic 11) is to use a two-dimensional "circle", which forms a torus-shaped "harmonic table":
| 0c | 400c | 800c | 0c | 400c | 800c | 0c |
| 480c | 880c | 80c | 480c | 880c | 80c | 480c |
| 960c | 160c | 560c | 960c | 160c | 560c | 960c |
| 240c | 640c | 1040c | 240c | 640c | 1040c | 240c |
| 720c | 1120c | 320c | 720c | 1120c | 320c | 720c |
| 0c | 400c | 800c | 0c | 400c | 800c | 0c |
| 480c | 880c | 80c | 480c | 880c | 80c | 480c |
| 960c | 160c | 560c | 960c | 160c | 560c | 960c |
| 240c | 640c | 1040c | 240c | 640c | 1040c | 240c |
| 720c | 1120c | 320c | 720c | 1120c | 320c | 720c |
| 0c | 400c | 800c | 0c | 400c | 800c | 0c |
We call this a torus because it wraps around from one side to the other, like if you were to print this on the surface of a donut.
Here,
- fifths are found by stepping 1 step up the Y-axis.
- harmonic sevenths are found by stepping 2 steps down the Y-axis.
- major thirds are found by stepping 1 step right along the X-axis.
Instead of two types of semitones, 15edo has four:
- the limma, found by stepping down and to the left by 1 on the table. This separates intervals belonging to different classes.
- the classical chroma, found by stepping down 1 and right 2 on the table. This separates intervals with the same class, but different qualities.
- the syntonic comma, found by stepping up 4 and left 1 on the table. This separates standard intervals from "wolf" intervals.
- the diaschisma, found by stepping up 4 and right 2 on the table. This separates fifth-generated "diatonic" intervals and their augmented or diminished zarlino counterparts. Note that this semitone is actually the complement of the just diaschisma, since the diaschisma proper is a negative interval in 15edo.
Scales
The Zarlino diatonic scale LmsLmLs or LsmLmLs is a way to preserve the classic major and minor dichotomies from 12edo. In the fourteen modes of these two scales, all thirds (i. e. intervals formable by ascending two scale-steps) are either major or minor, all fourths are either perfect fourths or large tritones, all fifths are perfect fifths or small tritones, and all sixths are either major or minor, with the following exceptions:
- in two of the fourteen modes, the fifth (i. e. interval formable by ascending four scale-steps) above the tonic is the 640c interval
- in two of the fourteen modes, the fourth is the 560c interval
- in two of the fourteen modes, the sixth is the 960c interval
- in two of the fourteen modes, the third is the 240c interval.
All of these exceptions involve intervals that can be better interpreted using intervals containing prime factors 7 and 11; thus, the Zarlino diatonic scale can bridge the classical 5-limit JI intervals with more complex intervals.
There is no MOS diatonic scale in 15edo, because a MOS diatonic scale is generated by stacking the fifth six times to get seven pitch classes, but in 15edo the process of stacking the fifth can only generate five pitch classes.
Non-diatonic scales
The scales generated by stacking the small major second, which are denoted "porcupine scales" due to their connection with the rank-2 regular temperament "porcupine", are onyx (├─┴─┴─┴──┴─┴─┴─┤) and pine (├─┴─┴─┴─┴┴─┴─┴─┤). The steps of the porcupine scales are minor tones. In onyx, four notes have perfect fifths above them, and four notes have perfect fourths, overlapping at one note which has both. Onyx has a special relationship to the diatonic scale, however, and this can be found by sharping the third and seventh degrees of onyx to produce the zarlino diatonic scale. The pine scale is simply the onyx scale with an extra note, which could function similarly to a "blue note" in blues.
The scales generated by stacking the 320-cent minor third are called smitonic (├┴──┴┴──┴┴──┴──┤) and 4L 7s (├┴┴─┴┴┴─┴┴┴─┴┴─┤), with the latter sort of functioning as a chromatic scale of the former. Smitonic contains a singular perfect fifth, where a 320-cent minor third and 400-cent major third span the same number of scale steps; in general, smitonic contains many intervals close to JI ratios in the 5-limit and 7-limit.
The scales generated by stacking either tritone are called pentic (├┴─────┴┴┴─────┤), antidiatonic (├┴┴────┴┴┴┴────┤), balzano (├┴┴┴───┴┴┴┴┴───┤), and 2L 9s (├┴┴┴┴──┴┴┴┴┴┴──┤).
After this, we have two special families of scales: augmented and blackwood. We will start off with blackwood.
Blackwood
Blackwood is based on our "fifth-generated diatonic" ├──┴──┴──┴──┴──┤. If we split each step of this scale into a larger and smaller portion, we get the blackwood scale proper: ├─┴┴─┴┴─┴┴─┴┴─┴┤. This scale has only two modes: major and minor, but it is extremely significant if you're used to diatonic harmony, since it has the unique property of always having either a major triad or a minor triad on any given note. In fact, by adding "missing" notes to zarlino to ensure that (which happen to themselves be in the shape of a major chord), we get blackwood. Thus, the blackwood scale can serve as an extremely powerful alternative to the absent MOS diatonic of this edo - it is, in a sense, a "purer" version of said system. (In other edos, this scale's relation to zarlino generalizes to that of blackdye, which loses some of its structural elegance in favor of a more direct diatonic connection and more in-tune intervals.)
Augmented
Augmented is, conversely, based on major thirds. The basic augmented scale is 15, which is equivalent to 12edo's augmented triad. We can follow the same formula as blackwood and split this scale into large and small steps to get the following possible combinations:
- ├───┴┴───┴┴───┴┤ - the augmented scale proper, which contains fifths on exactly three of the six notes. 12edo contains a tuning of this scale, but we usually don't talk about it in 12edo.
- ├──┴─┴──┴─┴──┴─┤ - the wholetone scale, which alternates the two sizes of wholetones and which contains many 7-limit intervals, but no fifths. This is similar to 12edo's wholetone scale, but since there are two different kinds of wholetones in 15edo, it uses both.
- ├─┴─┴┴─┴─┴┴─┴─┴┤ - the hyrulic scale, which is a way of combining the two prior scales to form a 9-note scale. This can be thought of as having perfect thirds, and major and minor fifths.
- ├──┴┴┴──┴┴┴──┴┴┤ - the tcherepnin scale, which is another combination of hard and soft triwood. This can also be thought of as having similar harmony to hyrulic, but with the minor fifth one step flatter.
MODMOS structures
Let's take the minor scale:
├──┴┴─┴──┴┴──┴─┤ - minor
A common way to alter the minor scale is to sharpen the sixth and/or seventh degrees, resulting in the harmonic and melodic minor and variations of Dorian:
├──┴┴─┴──┴┴───┴┤ - harmonic minor
├──┴┴─┴──┴─┴──┴┤ - dark melodic minor
├──┴┴─┴──┴──┴─┴┤ - bright melodic minor
├──┴┴─┴──┴─┴─┴─┤- "diatonyx" dorian
├──┴┴─┴──┴──┴┴─┤ - didymian dorian
A scale with a single generator (octave-equivalent, of course) is called a "MOS", and all these scales, including normal zarlino, are "MODMOSes" of onyx, formed by sharping or flatting a few notes of it respectively. While technically, because this is an equal tuning, any 7-note scale can be a MODMOS of onyx, I try to reserve it for scales that have harmonic commonalities with diatonic or with onyx.
Constructing chords and splitting steps
A more interesting way to construct scales is to stack chords rather than single intervals. For example, if we stack 3 major chords, we get:
├────┴───┴─────┤ (major chord on root)
+ ┌──┴─────┴────┴┐ (major chord on fifth)
+ ├─────┴────┴───┤ (major chord descending from root)
= ├──┴─┴┴──┴─┴──┴┤ - major
Surprise! Here's the zarlino scale again.
Let's try minor chords. This corresponds to flatting the seventh, third, and sixth degrees by one step.
├──┴┴─┴──┴┴──┴─┤- minor
In fact, this is actually how the normal major and minor scales are constructed in diatonic, so it's neat to see that it checks out here.
So instead, let's try a different chord (let's say, for some reason, you cared a lot about wolf chords).
├────┴──┴──────┤ (wolf major chord on root)
+ ┌┴──────┴────┴─┐ (wolf major chord on wolf fifth)
+ ├──────┴────┴──┤ (wolf major chord descending from root)
= ├┴───┴─┴┴───┴┴─┤ - wolf major
You can call this the "wolf major scale" because of how it's constructed.
Let's try a kind of diminished chord, called a wolf diminished chord, made of two different sizes of minor third. Since the chord is a lot narrower, we'll need 4 chords instead of 3 to build a reasonable scale.
├──┴───┴───────┤ (wolf diminished chord on root)
+ ┌──────┴──┴───┴┐ (wolf diminished chord on dim fifth)
+ ├───────┴──┴───┤ (wolf diminished chord descending from root)
+ ┌┴──┴───┴──────┐ (wolf diminished chord descending from aug fourth)
= ├┴─┴┴──┴┴─┴┴──┴┤- diminished
This scale also contains a "major wolf diminished" chord, which corresponds to the harmonic series sequence 5:6:7, much like a normal major chord corresponds to 4:5:6.
As can be seen, there's a lot of possibilities here.
Another way to build scales is by choosing a few key intervals, and splitting the jumps between them into steps. For example, we might decide that our key notes are 15.
Here, we have two large jumps that can be split into steps, and there's a couple ways to do this, including ones that just result in zarlino and ones that result in scales we haven't seen before.
├──┴─┴┴──┴──┴──┤- zaretan
├─┴──┴┴──┴──┴──┤ - legatus
├──┴─┴┴──┴──┴┴─┤- decurion
├─┴──┴┴──┴──┴┴─┤ - kaiser
If we choose a different set of key intervals, we get a different set of possible scales:
├──┴─┴──────┴──┤ =
├──┴─┴──┴─┴─┴──┤ - anhedonia
├──┴─┴─┴─┴─┴┴──┤ - mok
├────┴─┴────┴──┤ =
├──┴─┴─┴─┴──┴──┤- amsel
├───┴┴─┴───┴┴─┴┤ - drossel
Periodicity blocks
In 15edo, there are four primary ways of reaching the semitone on the harmonic table, corresponding to different copies of the semitone repeating periodically near the unison. It can be found as the difference between a stack of two fifths and a minor tone (the syntonic comma), the difference between a major third and a perfect fourth (the limma), the difference between the two tritones (the diaschisma), and the difference between a major and minor third (the classical chroma).
The standard zarlino scale can be defined by having the classical chroma and syntonic comma as its "chromas": if we create a tile that repeats at each multiple of these two chromas, the intervals within that tile are precisely those in the zarlino scale.
However, we can choose a different pair of semitones as our chromas, and get a different scale. Here's the classical chroma x diaschisma scale.
├──┴┴┴─┴┴─┴─┴┴┴┤ - elena
├──┴┴┴─┴─┴┴─┴┴┴┤ - kee'ra*
*Note: in just intonation, the kee'ra scale is a 7-limit "chair" scale, not a 5-limit periodicity block.
There are two variants as, since the diaschisma can be created by stacking two augmented fourths, the augmented fourth and diminished fifth fall precisely on the edge.
And the classical chroma x limma scale:
├───┴──┴──┴──┴─┤- myn
Regular temperaments
15edo shares Porcupine with 22edo, Augmented with 12edo, Semaphore with 19edo, and Blackwood with 10edo. It is also a tuning of Carlos Alpha, like 16edo.
Notation
Due to MOS-diatonic-based notations being nonfunctional with edos that have multiple chains of fifths (except for ups and downs notation, and even that requires E and F be treated as enharmonic), they are somewhat inconvenient for working with 15edo. Notation is often KISS notation based on onyx or pentawood, or notation based on the Zarlino diatonic scale.
