Interval space

A segment of octave-reduced 5-limit interval space. The origin is 1/1, and the axes represent 3/2 and 5/4. Highlighted is the diatonic scale.

An interval space is a multi-dimensional space in which intervals in just intonation or a regular temperament exist. The dimensionality or rank of an interval space is the minimum number of different "step sizes", called generators, that you need to stack to all the intervals in the space. An equal (rank-1) temperament has a 1D interval space, because any interval can be represented by one integer (the number of steps). A temperament such as Meantone has a 2D interval space (because it has both a generator and a period), so any interval must be represented with 2 integers (the number of periods and the number of generators), defining it as a rank-2 temperament. For just intonation, the number of primes in a JI subgroup determines its rank. For example, the 7-limit (subgroup 2.3.5.7) is rank-4, because intervals are composed from 4 primes: 2, 3, 5, and 7.

Monzos

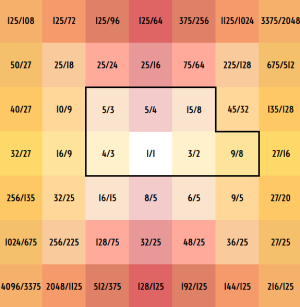
An interval's location in interval space is notated using a monzo. which functions as a list of coordinates. In just intonation, a monzo encodes the prime factorization of an interval's frequency ratio as a list of exponents. For example, 125/96 is 2^-5 * 3^-1 * 5^3, so the monzo is [-5 -1 3⟩. In general, [n₁ n₂ n₃ ... n_k⟩ means 2^n₁ * 3^n₂ * 5^n₃ * ... * p^n_k for k-th prime p.

In a temperament, a monzo can be defined with respect to a set of generators (since the same temperament may have multiple valid sets of generators). For example, the monzo for ~5/4 in Meantone with generators ~2 and ~3/2 is [-2 4⟩, but with generators ~2, ~3 it is [-6 4⟩.

When stacking intervals, simply add the corresponding entries of their monzos. For example, 125/96 * 81/64 = [-5 -1 3⟩ + [-6 4 0⟩ = [-11 3 3⟩ = 3375/2048.