Aberrisma
An aberrisma is an interval between roughly 20 and 55 cents representing some comma as an additional smaller type of melodic step (that is, a diesis). The aberrisma is used as one of the parameters in constructing an aberrismic scale, a type of ternary scale. For example, blackdye is a 10-note aberrismic superset of the 7-note nicetone, but with a more distinctive set of three step sizes and added opportunities to avoid pythagorean and wolf intervals.
Aberrismic theory is the subset of microtonal theory pioneered by Ground and Inthar that deals with aberrismas.
Example: The emergence of blackdye
The Zarlino diatonic is chiral - there are two different, equally valid second degrees of the Ionian mode. Both are useful, as the sharp one forms a perfect fifth with the fifth degree but a wolf fifth with the sixth degree, and the flat one forms a perfect fifth with the sixth degree but a wolf fifth with the fifth degree.
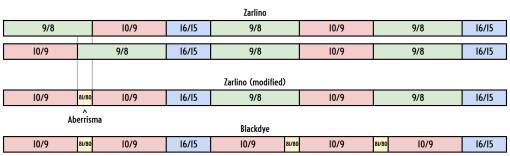
One way to make it achiral is to temper out 81/80, the difference between these two steps, resulting in meantone diatonic; intuitively this requires flattening the fifth and sharpening the sixth somewhat. However, an alternative way, if you wish to observe 81/80 or to use just intonation, is to include both varieties of whole tone over the unison, treating 81/80 as a melodic step between them. This can be thought of as dividing up a 9/8 into a 10/9 and an 81/80. It is then reasonable to extend this action to all instances of 9/8 in the scale (as, for instance, the Didymic diatonic has 27/16 as opposed to 5/3). The result is a 10-note ternary scale called blackdye.
The "why" of aberrismic theory
This section will attempt to describe the principles and stylistic features of a specific style of music that justify aberrismic theory. It is not an attempt to present aberrismic theory as absolute truth.
- A style of music that is melodic and heavy in modulations benefits from
- Multiple step sizes for melodic interest, for example diesis-sized steps that are below conventional semitones, specifically ones large enough to be melodically distinct but small enough to represent intonational changes.
- A set of modulatory intervals, including fifths.
- A system that allows unlimited modulation.
- It is widely agreed that lower primes are more robust to detuning. Hence for approximating JI with edos, we use lower prime temperaments, and which also represent either 81/80 or 64/63 steps for greater accuracy.
The above suggests temperaments, in particular edos, that use tempered lower primes, and edos large enough to have small diesis-sized steps. In the context of fifth-based modulation, scales also benefit from having offset arcs of fifths. One simple way to have this is to detemper MOS scales into ternary scales with an additional smaller melodic step size, which have a generator arc with fifths or a generator arc that stacks to fifths via a detempered generator chain.
List of aberrismic scales
- "GS(...)[n]" is generator sequence notation.
- The word "by" denotes the cross-set.
- "subst ax(bycz)" denotes MOS substitution.
- ≈ denotes that one or two notes are missing from the full cross-set and one note may have been added.
- Under "Patterns", "C" is achiral, and "R" and "L" denote two chiralities of a chiral pair.
Quasi-diatonic aberrismic scales
| Name / Signature | Pattern(s) | Possible JI interp. | Generator-offset structure (interpreted) |
Notes |
|---|---|---|---|---|
| pinedye / dia1s (5L2m1s) subst 5L(2m1s) |
1sC: LLsLLmLm 1sR: LLmLLmLs 1sL: LLmLLsLm |
2.3.5 [L, m, s] = [10/9, 27/25, 81/80] |
≈ GS(3/2)[3] by GS(10/9)[3] | 1sC has 4 fifths and 1sR/1sL have 5 |
| diasem / dia2s (5L2m2s) subst 5L(2m2s) |
2sR: LmLsLmLsL 2sL: LsLmLsLmL |
2.3.7 [L, m, s] = [9/8, 28/27, 64/63] |
≈ GS(3/2)[5] by 7/6 | Aggregate generator is 4/3, thus has fifth arcs of 5 and 4 notes respectively |
| blackdye / dia3s (5L2m3s) subst 5L(2m3s) |
sLmLsLmLsL | 2.3.5 [L, m, s] = [10/9, 16/15, 81/80] |
GS(3/2)[5] by 10/9 | Two interleaved 3-limit pentatonics |
| diaslen / dia4s (5L2m4s) subst 5L(2m4s) |
4sC: LmLsLsLmLss 4sR: LsLmLsLsLms 4sL: LsLsLmLsLsm |
2.3.7 [L, m, s] = [9/8, 49/48, 64/63] |
≈ GS(3/2)[4] by GS(8/7)[3] | Fifth arcs with 4 notes, 4 notes, and 3 notes, with offset 8/7. Tempered to the slentonic {5L6s) MOS by Slendric. Detempered Slendric[11] generator structure, aggregate generator is 3/2 |
| chromedye / dia5s (5L2m5s) |
5sC: LsLsLmsLsLsm (subst 2m(5L5s)) 5sR: LmsLsLsLmsLs 5sL: LsLsLsmLsLsm |
5120/5103-tempered 2.3.5.7 [L, m, s] = [10/9, 256/243, 81/80] |
5sC: GS(3/2)[6] by 40/27 5sR and 5sL: superimposition of GS(3/2)[5] and GS(3/2)[7] |
Fifth-generated but with a 6-step offset |
| whitedye / dia7s (5L2m7s) subst 7s(5L2m) |
LsLsLsmsLsLsms | 5120/5103-tempered 2.3.5.7 [L, m, s] = [10/9, 28/27, 81/80] |
GS(3/2)[7] by 81/80 | Two interleaved diatonics |
Other aberrismic scales
| Name / Signature | Pattern(s) | Possible JI/erac interp. | Generator-offset structure (interpreted) |
Notes |
|---|---|---|---|---|
| penslen / slen5m (5L5m6s) subst 6s(5L5m) |
LmsLmsLsmLsmLsms | 2.3.5.7.11[41 & 46] [L, m, s] = [12/11, 33/32, 64/63] |
GS(8/7)[8] by 11/8 | Has two aberrisma sizes, s and m. |
| arm5s (7L2m5s) subst 7L(2m5s) |
LmLsLsLmLsLsLs | 2.x<3.5.7.11.13[37edo] (4:2:1) | GS(<<3/2)[7] by 14/13 | An interleaving of two antidiatonic scales. |
| mosh3s (3L4m3s) subst 4m(3L3s) |
LmsLmsmLsm | 2.x<3.7.11.13[37edo] (5:4:2) | GS(16/13)[5] by 11/8 | |
| smi2s (4L3m2s) subst 2s(4L3m) |
C: LLmsLmLsm R: LmLmsLmLs L: LmLsLmLsm |
2.9.7.11.17[46edo] (8:4:1) | ≈ GS(17/14)[3] by GS(11/8)[3] (exact for C) | |
| smi2m? (4L2m3s) subst 2m(4L3s) |
C: LLsmLsLms R: LmLsLmsLs L: LmLsLsmLs |
2.5.7 [L, m, s] = [28/25, 35/32, 50/49] |
≈ GS(5/4)[3] by GS(7/5)[3] (exact for C) | Didacus tempering makes L = m + s. |
Systematic naming
Basic systematic names for aberrismic scales are of the form
[mos_prefix]n[added_step_size] (e.g. dia2s for diasem),
where the MOS prefix (a TAMNAMS prefix if one is available) is chosen based on the aberrismic-theoretical generator (as opposed to the offset), rather than from any particular mathematical construction. For example, penslen has MOS substitution type 6s(5L5m), but the systematic name is slen5m, not penwd6s, since the generator is conceived as a generator of 5L6s (Slendric[11]).
This is subject to change as aberrismic theory notation is updated in the future.
Notation
Aberrismic notation restricts to diatonic notation on the tempered 3-limit.
Aberrismic/straddle-prime accidentals:
- Plus / Minus +/- : These tune a note sharp or flat by a small aberrisma. They reference Johnston notation because 81/80 is a common aberrisma, but they can also represent 64/63 or any other interval of similar function. They're also used to denote straddle primes, like 3+ and 3- (in a straddle-3 subgroup, these can be abbreviated as 3±). This results in some pretty heavy overloading, but +/- are only used on notes when they represent an aberrisma and only used on ratios when they represent straddle primes.
- Duplus / Duminus ≠/= : Short for ++/--, most often representing 36/35~33/32~1053/1024, which is the large aberrisma in scales like penslen, or two small aberrismas in Akea temperament. Of all options, this set of characters is the easiest to type, looks the best in various fonts, and is least likely to be confused for the similar semisharp accidental (although they happen to represent the same size of interval).
Aberrismic theory and RTT
Aberrismic theory often applies RTT to ternary LCJI scales with comma steps. Certain scales with aberrismas may thus be endowed with JI interpretations via RTT temperaments, which may be used in suitable equal temperaments. Under groundfault's use of edos (usually patent vals) as RTT temperaments, the aberrisma tends to become a 81/80 in a 2.3.5 context and a 64/63 in a 2.3.7 context. Some scales such as 5L2m5s and 5L2m7s admit a more accurate 2.3.5.7 interpretation that tempers out neither 81/80 nor 64/63 but identifies the two commas, tempering out 5120/5103. Tempering is important in aberrismic theory as a way to improve the function of commas (frequently 81/80 or 64/63) as aberrismas in ternary LCJI scales by tempering them larger than just.
At times, a scale pattern has varying temperaments according to the tuning. For example, 5L2m3s may be given the temperament structure of either untempered 2.3.5 or Ultrapyth temperament.
There are two choices involved in interpreting a given ternary scale, namely the choice of temperament and the choice of where to map the scale steps. The assignment of scale steps to tempered intervals is chosen to improve coverage of important LCJI intervals.
Example: Blackdye
The following table shows two different temperament interpretations for the same aberrismic scale pattern blackdye (sLmLsLmLsL), under untempered 2.3.5 and Ultrapyth respectively.
- Untempered does not mean that the final tuning must be the JI tuning, but simply that there exists an exact JI tuning.
- Ultrapyth, 2.3.5.7.11.13[32 & 37], is a diatonic temperament generated by a fifth even sharper than in Superpyth. 37edo provides a nearly optimal tuning. Note that we chose to regard the 3-step 2L + s as a 14/11 rather than as a 5/4, lest the interpretation merely be an extension of the untempered 2.3.5 one. groundfault terms the tuning of blackdye that makes aberrisma-altered Pyth thirds 13/11 and 14/11 Flutterpyth blackdye.
| Interval class | Sizes | Untempered 2.3.5 | 2.3.7.11.13 Flutterpyth (extended to 13-limit Ultrapyth) |
|---|---|---|---|
| 1-step | s m L |
81/80 16/15 10/9 |
143/140 22/21 160/143 |
| 2-step | L + s L + m |
9/8 32/27 |
8/7, 9/8 7/6 |
| 3-step | L + 2s L + m + s 2L + s 2L + m |
729/640 6/5 5/4 320/243 |
7/6 13/11 14/11 13/10 |
| 4-step | 2L + 2s 2L + m + s |
81/64 4/3 |
13/10 4/3 |
| 5-step | 2L + m + 2s 2L + 2m + s 3L + 2s 3L + m + s |
27/20 64/45 45/32 40/27 |
66/49 11/8 16/11 49/33 |
| 6-step | 3L + m + 2s 3L + 2m + s |
3/2 128/81 |
3/2 20/13 |
| 7-step | 3L + m + 3s 3L + 2m + 2s 4L + m + 2s 4L + 2m + s |
243/160 8/5 5/3 1280/729 |
20/13 11/7 22/13 12/7 |
| 8-step | 4L + m + 3s 4L + 2m + 2s |
27/16 16/9 |
12/7 7/4, 16/9 |
| 9-step | 5L + 2m + s 5L + m + 2s 4L + 2m + 2s |
9/5 15/8 160/81 |
143/80 21/11 280/143 |
Glossary
- Aberration scale: A scale made by interleaving aberrismas into a binary scale and stretching or compressing, usually a MOS substitution scale of type [a+b+1]s(aLbm) (compression, called tractaberrated) or [a+b-1]s(aLbm) (stretching, called tensaberrated). For example, sLsmsLsLsLsmsLs is an aberration scale made from diatonic (a MOS substitution scale of type 8s(5L2m)).
- Aberrisma: The smallest interval region that melodically sounds like a step.
- Magnitone: The melodic function of L + s in quasi-diatonic aberrismic scales.
- Monotone-MOS: A ternary scale is monotone-MOS if it becomes a MOS under all three of the identifications L = M, M = s, and s = 0. If any (not necessarily all) of the identifications make the scale a MOS, the scale is said to satisfy a monotone-MOS condition. For example, diasem (LmLsLmLsL) satisfies all three monotone-MOS conditions, but blackdye (sLmLsLmLsL) satisfies only the m = s and s = 0 monotone-MOS conditions. An aberrismic scale is required to satisfy the s = 0 monotone-MOS condition.
- Solitone: The melodic function of the L step in quasi-diatonic aberrismic scales.
- Subaberrisma: A step so small (smaller than an aberrisma) that its status as a melodic step is unclear.
